2024年中考數(shù)學(xué)復(fù)習(xí)：三角函數(shù)

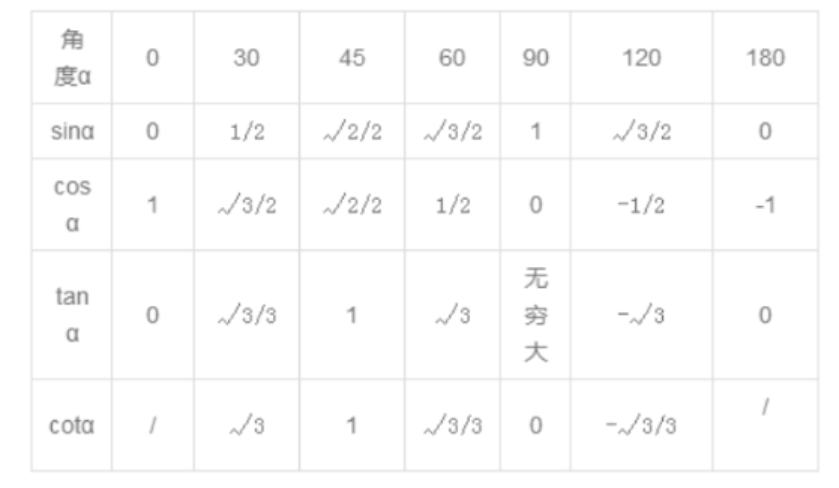
特殊角三角函數(shù)值

三角和的公式

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

兩角和差公式

sin(A+B) = sinAcosB+cosAsinB

sin(A-B) = sinAcosB-cosAsinB

cos(A+B) = cosAcosB-sinAsinB

cos(A-B) = cosAcosB+sinAsinB

tan(A+B) = (tanA+tanB)/(1-tanAtanB)

tan(A-B) = (tanA-tanB)/(1+tanAtanB)

cot(A+B) = (cotAcotB-1)/(cotB+cotA)

cot(A-B) = (cotAcotB+1)/(cotB-cotA)

三角函數(shù)關(guān)系

互余角的關(guān)系

sin(90°-α)=cosα, cos(90°-α)=sinα,

tan(90°-α)=cotα, cot(90°-α)=tanα.

平方關(guān)系

sin^2(α)+cos^2(α)=1

tan^2(α)+1=sec^2(α)

cot^2(α)+1=csc^2(α)

積的關(guān)系

sinα=tanα·cosα

cosα=cotα·sinα

tanα=sinα·secα

cotα=cosα·cscα

secα=tanα·cscα

cscα=secα·cotα

倒數(shù)關(guān)系

tanα·cotα=1

sinα·cscα=1

cosα·secα=1

誘導(dǎo)公式

誘導(dǎo)公式的本質(zhì)

所謂三角函數(shù)誘導(dǎo)公式，就是將角n·(π/2)±α的三角函數(shù)轉(zhuǎn)化為角α的三角函數(shù)。

常用的誘導(dǎo)公式

公式一：設(shè)α為任意角，終邊相同的角的同一三角函數(shù)的值相等：

sin(2kπ+α)=sinα k∈z

cos(2kπ+α)=cosα k∈z

tan(2kπ+α)=tanα k∈z

cot(2kπ+α)=cotα k∈z

公式二：設(shè)α為任意角，π+α的三角函數(shù)值與α的三角函數(shù)值之間的關(guān)系：

sin(π+α)=-sinα

cos(π+α)=-cosα

tan(π+α)=tanα

推導(dǎo)公式

tanα+cotα=2/sin2α

tanα-cotα=-2cot2α

1+cos2α=2cos^2α

1-cos2α=2sin^2α

1+sinα=(sinα/2+cosα/2)^2

和差化積公式：

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]

積化和差公式：

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

降冪公式

sin^2(α)=(1-cos(2α))/2=versin(2α)/2

cos^2(α)=(1+cos(2α))/2=covers(2α)/2

tan^2(α)=(1-cos(2α))/(1+cos(2α))

公式：

sinα=2tan(α/2)/[1+tan^2(α/2)]

cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]

tanα=2tan(α/2)/[1-tan^2(α/2)]

三倍角公式：

sin(3α)=3sinα-4sin^3(α)

cos(3α)=4cos^3(α)-3cosα

tan3α=(3tanα-tan^3(α))/(1-3tan^2(α))

半角公式：

sin(α/2)=±√((1-cosα)/2)

cos(α/2)=±√((1+cosα)/2)

tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα

輔助角公式

Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中

sint=B/(A^2+B^2)^(1/2)

cost=A/(A^2+B^2)^(1/2)

tant=B/A

Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

       編輯推薦：

       2024年中考各科目重點(diǎn)知識(shí)匯總

　　 歡迎使用手機(jī)、平板等移動(dòng)設(shè)備訪問中考網(wǎng)，2023中考一路陪伴同行！>>點(diǎn)擊查看